P1099 [NOIP 2007 提高组] 树网的核

题目描述

设 $T=(V,E,W)$ 是一个无圈且连通的无向图（也称为无根树），每条边都有正整数的权，我们称 $T$ 为树网（treenetwork），其中 $V$，$E$ 分别表示结点与边的集合，$W$ 表示各边长度的集合，并设 $T$ 有 $n$ 个结点。

路径：树网中任何两结点 $a$，$b$ 都存在唯一的一条简单路径，用 $d(a, b)$ 表示以 $a, b$ 为端点的路径的长度，它是该路径上各边长度之和。我们称
$d(a, b)$ 为 $a, b$ 两结点间的距离。

$D(v, P)=\min{d(v, u)}$, $u$ 为路径 $P$ 上的结点。

树网的直径：树网中最长的路径成为树网的直径。对于给定的树网 $T$，直径不一定是唯一的，但可以证明：各直径的中点（不一定恰好是某个结点，可能在某条边的内部）是唯一的，我们称该点为树网的中心。

偏心距 $\mathrm{ECC}(F)$：树网 $T$ 中距路径 $F$ 最远的结点到路径 $F$ 的距离，即

$$\mathrm{ECC}(F)=\max{D(v, F),v \in V}$$

任务：对于给定的树网 $T=(V, E, W)$ 和非负整数 $s$，求一个路径 $F$，他是某直径上的一段路径（该路径两端均为树网中的结点），其长度不超过 $s$（可以等于 $s$），使偏心距 $\mathrm{ECC}(F)$ 最小。我们称这个路径为树网 $T=(V, E, W)$ 的核（Core）。必要时，$F$ 可以退化为某个结点。一般来说，在上述定义下，核不一定只有一个，但最小偏心距是唯一的。

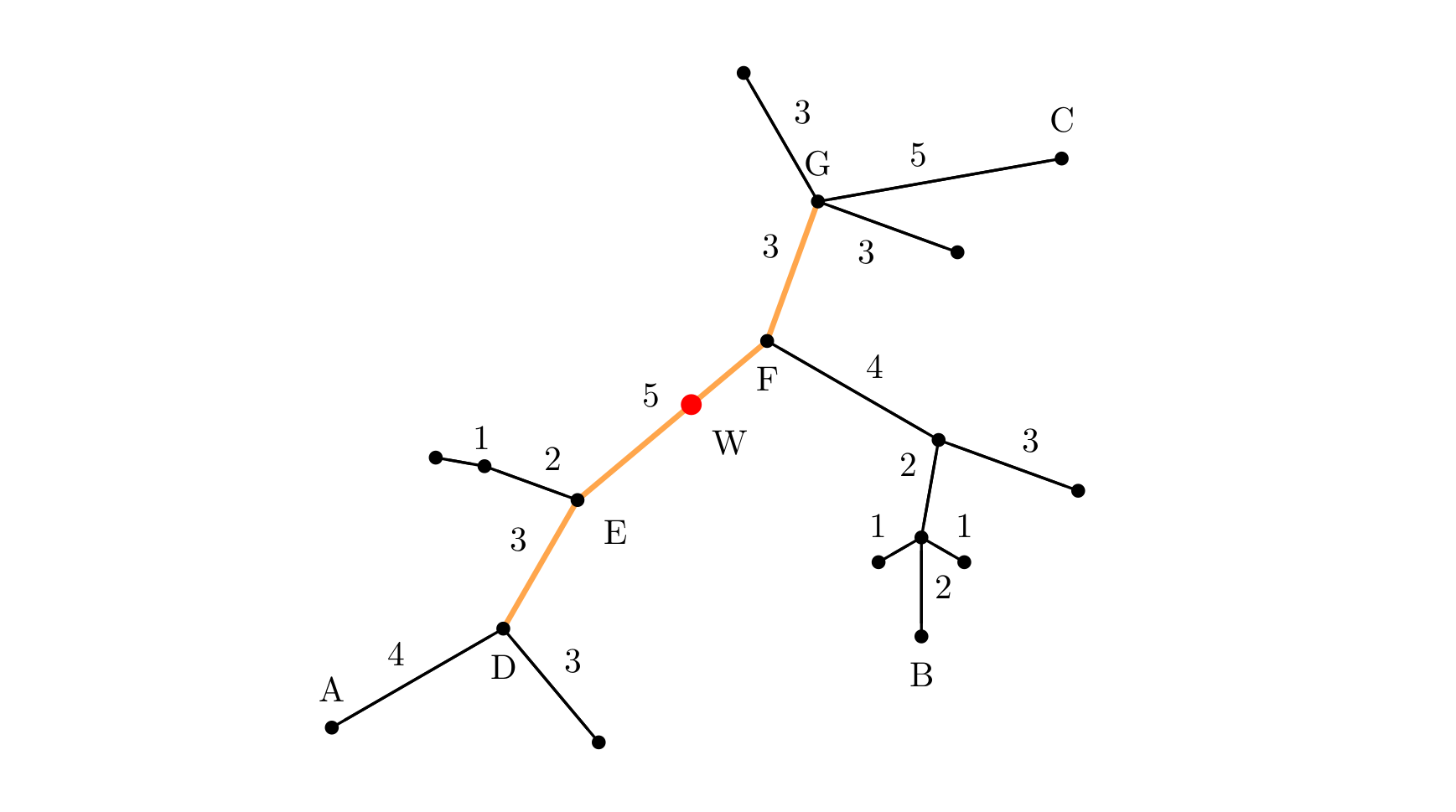
下面的图给出了树网的一个实例。图中，$A-B$ 与 $A-C$ 是两条直径，长度均为 $20$。点 $W$ 是树网的中心，$EF$ 边的长度为 $5$。如果指定 $s=11$，则树网的核为路径DEFG（也可以取为路径DEF），偏心距为 $8$。如果指定 $s=0$（或 $s=1$、$s=2$），则树网的核为结点 $F$，偏心距为 $12$。

输入格式

共 $n$ 行。

第 $1$ 行，两个正整数 $n$ 和 $s$，中间用一个空格隔开。其中 $n$ 为树网结点的个数，$s$ 为树网的核的长度的上界。设结点编号以此为 $1,2\dots,n$。

从第 $2$ 行到第 $n$ 行，每行给出 $3$ 个用空格隔开的正整数 $u, v, w$，依次表示每一条边的两个端点编号和长度。例如，2 4 7 表示连接结点 $2$ 与 $4$ 的边的长度为 $7$。

输出格式

一个非负整数，为指定意义下的最小偏心距。

输入输出样例 #1

输入 #1

1
2
3
4
5
5 2
1 2 5
2 3 2
2 4 4
2 5 3

输出 #1

1
5

输入输出样例 #2

输入 #2

1
2
3
4
5
6
7
8
8 6
1 3 2
2 3 2 
3 4 6
4 5 3
4 6 4
4 7 2
7 8 3

输出 #2

1
5

说明/提示

  • 对于 $40%$ 的数据，保证 $n \le 15$。
  • 对于 $70%$ 的数据，保证 $n \le 80$。
  • 对于 $100%$ 的数据，保证 $2\le n \le 300$，$0\le s\le10^3$，$1 \leq u, v \leq n$，$0 \leq w \leq 10^3$。

NOIP2007 提高组第四题

题解

先整理一下树的有关结论：

树上的距离

  • 点到点：任意两点之间都存在唯一简单路径 d(a, b)(在树上体现为”不走回头路”) 为路径上各边长度之和
  • 点到直线：一点到该路径上各点的最小值是距离
  • 偏心距：树网 T 中距路径 F 最远的结点到路径 F 的距离

树的直径

  • 求法：2次dfs，任意一点到最远点，那个最远点即为直径的一端点，再求这个端点到最远点，这一最远点即为另一端点
  • 易知，非直径上的点沿着不经过直径的路径，只可能通向唯一一个在某一条确定直径上的点，否则有环，而树上无环
  • 重要性质，直径上的任意一点，所能到达的最远点，总是直径的端点

解题步骤

  1. 求出直径端点 (2次dfs)
  2. 双指针法求直径两端点到区间两端点距离的最大值, 区间长度不超过s；记录这一最大值集合中的最小值
  3. 统计直径上每个点到非直径上点的距离最大值，dfs过程中不经过直径上的其他点
  4. 答案在2、3步所得中取最大值

说明：为什么最小偏心距结果却是这些值中的最大值？为什么step2要取最小值？

  • 如果遇到一个极大的dis[i]
  • 我们的区间要么包含这个很大的dis[i] 要么我们将区间移动至不包含i结点的部分
  • 但由树的直径[[树的直径|重要性质]]，此时我们的区间端点到直径端点的距离甚至比刚才的dis[i]还大 故不能出此下策
  • 两害相较取其轻 我们的答案一定在max(ans, dis[i])中产生
  • 这也是为什么前面我们要取直径两端到区间端点距离的最小值 因为更大的值会大于等于后面的dis[i] 我们不用再考虑那么长的距离

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
using namespace std;
#define MAXN 500000+10
int n, s, ans = MAXN * 1000, far;
int dis[MAXN], fa[MAXN], flag[MAXN];
struct edge
{
    int to, w;
};
vector<edge> G[MAXN];
void dfs(int u, int f) {
    fa[u] = f;
    if(dis[u]>dis[far]) far = u; // 记录最远距离
    for(int i=0; i<G[u].size(); i++) {
        if(G[u][i].to == f || flag[G[u][i].to]) continue;
        dis[G[u][i].to] = dis[u] + G[u][i].w;
        dfs(G[u][i].to, u);
    }
}
int main() {
    scanf("%d%d", &n, &s);
    for(int i=1; i<n; i++) {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        G[u].push_back({v, w});
        G[v].push_back({u, w}); 
    }
    int A, B; // 直径的两端
    dis[1] = 0;
    dfs(1, 0);
    A = far;
    dis[far] = 0;
    dfs(far, 0);
    B = far;
    for(int i=B, j=B; i; i=fa[i]) {
        while (dis[j]-dis[i] > s) 
        {
            j = fa[j]; // 一旦距离超过s 缩短距离
        }
        int x = max(dis[i], dis[B]-dis[j]);
        ans = min(ans, x);
    }
    for (int i=B; i!=0; i=fa[i]) {
        flag[i] = 1;
    }
    for(int i=B; i!=0; i=fa[i]) {
        dis[i] = 0;
        dfs(i, fa[i]); // 由树的性质可知，dis[i]一经标定后不会再被覆盖
    }
    for(int i=1; i<=n; i++) {
        ans = max(ans, dis[i]); // 利用任意一点到直径端点的距离最长的结论可以证明这样标是正确的
    }
    printf("%d\n", ans);
    return 0;
}