组合数与杨辉三角
P2822 [NOIP 2016 提高组] 组合数问题
题目背景
NOIP2016 提高组 D2T1
题目描述
组合数 $\binom{n}{m}$ 表示的是从 $n$ 个物品中选出 $m$ 个物品的方案数。举个例子,从 $(1,2,3)$ 三个物品中选择两个物品可以有 $(1,2),(1,3),(2,3)$ 这三种选择方法。根据组合数的定义,我们可以给出计算组合数 $\binom{n}{m}$ 的一般公式:
$$\binom{n}{m}=\frac{n!}{m!(n-m)!}$$
其中 $n!=1\times2\times\cdots\times n$;特别地,定义 $0!=1$。
小葱想知道如果给定 $n,m$ 和 $k$,对于所有的 $0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )$ 有多少对 $(i,j)$ 满足 $k\mid\binom{i}{j}$。
输入格式
第一行有两个整数 $t,k$,其中 $t$ 代表该测试点总共有多少组测试数据,$k$ 的意义见问题描述。
接下来 $t$ 行每行两个整数 $n,m$,其中 $n,m$ 的意义见问题描述。
输出格式
共 $t$ 行,每行一个整数代表所有的 $0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )$ 中有多少对 $(i,j)$ 满足 $k\mid\binom{i}{j}$。
输入输出样例 #1
输入 #1
1 | 1 2 |
输出 #1
1 | 1 |
输入输出样例 #2
输入 #2
1 | 2 5 |
输出 #2
1 | 0 |
说明/提示
【样例1说明】
在所有可能的情况中,只有 $\binom{2}{1} = 2$ 一种情况是 $2$ 的倍数。
【子任务】
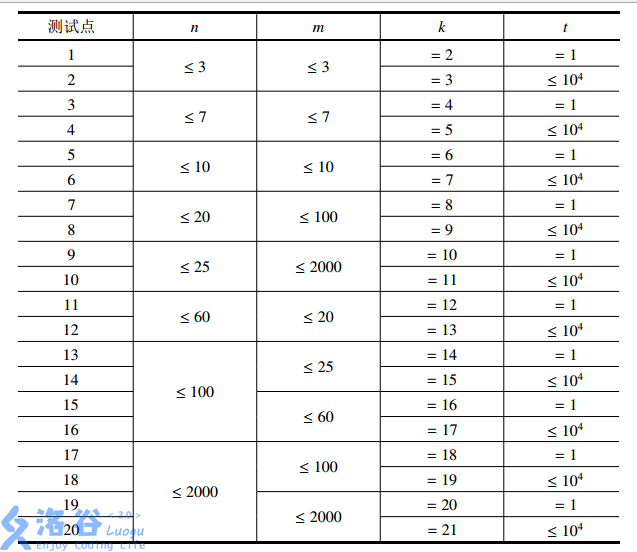
- 对于全部的测试点,保证 $0 \leq n, m \leq 2 \times 10^3$,$1 \leq t \leq 10^4$。
题解
代码示例与注释
1 |
|
注意
- 本题使用了杨辉三角递推地计算组合数
- 还使用了二维前缀和优化了求解过程
- 注意本题要求的是可以被k整除的情况 答案mod k即可
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 Spring Garden!
